Assignment 2 (Regular Expressions, Automata, Conversions)

1. Consider the following languages over alphabet { a, b }:

   L1 = set of words that start and end with the same symbol

   L2 = set of words of odd length

   The DFAs for L1 and L2 are shown below:

   

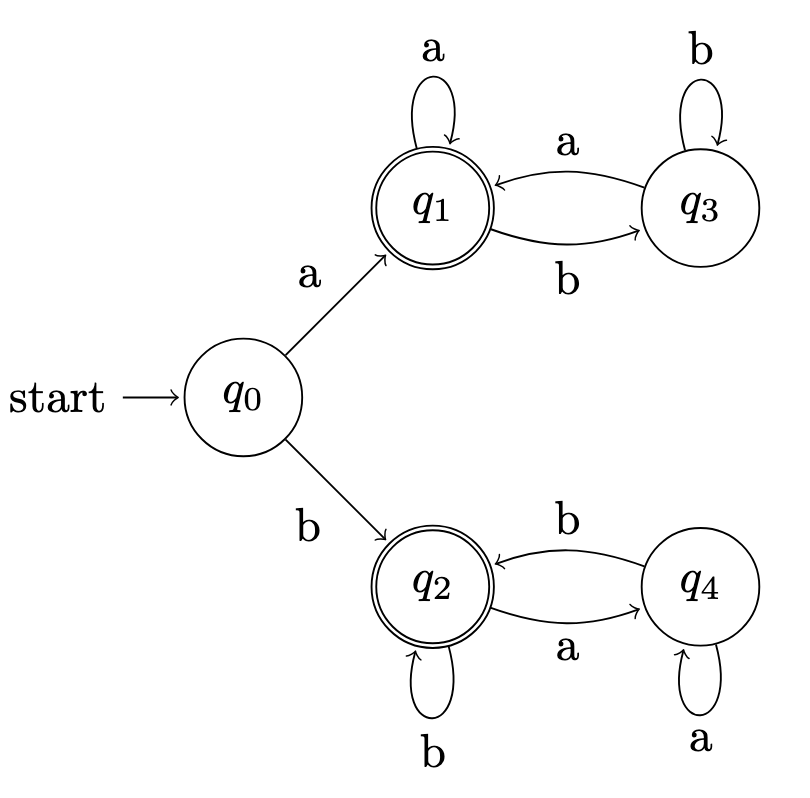
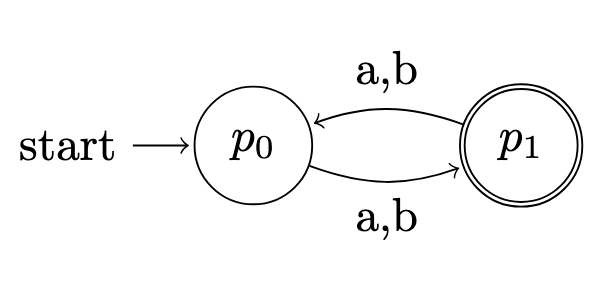
   Construct DFAs for the following languages:

   1. L1 ∪ L2

      

   2. L1 . L2

      

      e-closure of states:

      q0 {'q0'}
      q1 {'p0', 'q1'}
      q2 {'p0', 'q2'}
      q3 {'q3'}
      q4 {'q4'}
      
      p0 {'p0'}
      p1 {'p1'}
      

      Applying RMET, we get the following NFA without empty transitions:

      start q0
      final p1 
      trans q0:a:q1
      trans q0:a:p0
      trans q0:b:p0
      trans q0:b:q2
      trans q1:a:p1
      trans q1:a:q1
      trans q1:a:p0
      trans q1:b:p1
      trans q1:b:q3
      trans q2:a:p1
      trans q2:a:q4
      trans q2:b:p1
      trans q2:b:p0
      trans q2:b:q2
      trans q3:a:q1
      trans q3:a:p0
      trans q3:b:q3
      trans q4:a:q4
      trans q4:b:p0
      trans q4:b:q2
      trans p0:a:p1
      trans p0:b:p1
      trans p1:a:p0
      trans p1:b:p0
      

      Applying NTD, we get the following DFA:

      start q0
      final p0_p1_q3 p1_q3 p0_p1_q1 p1_q4 p0_p1_q4 p0_p1_q2 
      trans q0:a:p0_q1
      trans q0:b:p0_q2
      trans p0_q1:a:p0_p1_q1
      trans p0_q1:b:p1_q3
      trans p0_q2:a:p1_q4
      trans p0_q2:b:p0_p1_q2
      trans p0_p1_q1:a:p0_p1_q1
      trans p0_p1_q1:b:p0_p1_q3
      trans p1_q3:a:p0_q1
      trans p1_q3:b:p0_q3
      trans p1_q4:a:p0_q4
      trans p1_q4:b:p0_q2
      trans p0_p1_q2:a:p0_p1_q4
      trans p0_p1_q2:b:p0_p1_q2
      trans p0_p1_q3:a:p0_p1_q1
      trans p0_p1_q3:b:p0_p1_q3
      trans p0_q3:a:p0_p1_q1
      trans p0_q3:b:p1_q3
      trans p0_q4:a:p1_q4
      trans p0_q4:b:p0_p1_q2
      trans p0_p1_q4:a:p0_p1_q4
      trans p0_p1_q4:b:p0_p1_q2
      

   3. L1^*

      

      e-closure of states:

      q5 {'q0', 'q5'}
      q0 {'q0'}
      q1 {'q0', 'q1', 'q5'}
      q2 {'q0', 'q2', 'q5'}
      q3 {'q3'}
      q4 {'q4'}
      

      Applying RMET, we get the following NFA without empty transitions:

      start q5
      final q2 q5 q1 
      trans q5:b:q2
      trans q5:b:q5
      trans q5:b:q0
      trans q5:a:q5
      trans q5:a:q0
      trans q5:a:q1
      trans q0:b:q2
      trans q0:b:q5
      trans q0:b:q0
      trans q0:a:q5
      trans q0:a:q0
      trans q0:a:q1
      trans q1:b:q2
      trans q1:b:q5
      trans q1:b:q3
      trans q1:b:q0
      trans q1:a:q5
      trans q1:a:q0
      trans q1:a:q1
      trans q2:b:q2
      trans q2:b:q5
      trans q2:b:q0
      trans q2:a:q5
      trans q2:a:q4
      trans q2:a:q1
      trans q2:a:q0
      trans q3:b:q3
      trans q3:a:q5
      trans q3:a:q0
      trans q3:a:q1
      trans q4:b:q2
      trans q4:b:q5
      trans q4:b:q0
      trans q4:a:q4
      

      Applying NTD, we get the following DFA:

      start q5
      final q0_q1_q5 q0_q2_q3_q5 q5 q0_q2_q5 q0_q1_q4_q5 
      trans q5:a:q0_q1_q5
      trans q5:b:q0_q2_q5
      trans q0_q1_q5:a:q0_q1_q5
      trans q0_q1_q5:b:q0_q2_q3_q5
      trans q0_q2_q5:a:q0_q1_q4_q5
      trans q0_q2_q5:b:q0_q2_q5
      trans q0_q2_q3_q5:a:q0_q1_q4_q5
      trans q0_q2_q3_q5:b:q0_q2_q3_q5
      trans q0_q1_q4_q5:a:q0_q1_q4_q5
      trans q0_q1_q4_q5:b:q0_q2_q3_q5
      

   Hint: You may construct intermediate NFAs and then use RMET and NTD algorithms to convert to DFAs. For the ∪ language, you may use the Product DFA construction.

2. Use the MIN algorithm to minimize the following DFA:

   start A
   final C F I
   trans A:0:B
   trans A:1:B
   trans B:0:C
   trans B:1:F
   trans C:0:D
   trans C:1:H
   trans D:0:E
   trans D:1:H
   trans E:0:F
   trans E:1:I
   trans F:0:G
   trans F:1:B
   trans G:0:H
   trans G:1:B
   trans H:0:I
   trans H:1:C
   trans I:0:A
   trans I:1:E