Tuples¶
A tuple is a value that contains a fixed number of elements, each with a distinct type.
Tuples are immutable.
Tuples are especially handy for returning multiple values from a method.
val student = ("Jones",3.8,"CS")
student._1
student._2
student._3
val (name,gpa,major) = student
println(name)
println(gpa)
println(major)
val numPairs = List((2, 5), (3, -7), (20, 56))
numPairs map (x => x._1*x._2)
// for ((a, b) <- numPairs) yield a*b
Case Classes¶
Case classes are used in Scala to model immutable objects.
These are very useful when writing purely functional code.
Look like regular classes from Object-Oriented World, but with short cut notation
case class Student(name: String, gpa: Double, major: String)
val s1 = Student("Jones",3.4,"CSC")
val s2 = Student("Smith",3.6,"MATH")
val s3 = Student("Gary",3.3,"CSC")
println(s1.name)
abstract class BT
case class Tree(left: BT, value: Int, right: BT) extends BT
object Nil extends BT
// val t11 = Nil
// val t12 = Tree(Nil,10,Nil)
// val t13 = Tree(Tree(Nil,5,Nil),10,Nil)
def memberBST(x: Int, t: BT): Boolean = t match {
case Nil => false
case Tree(left,value,right) if (x == value) => true
case Tree(left,value,right) if (x < value) => memberBST(x,left)
case Tree(left,value,right) if (x > value) => memberBST(x,right)
}
def insertBST(x: Int, t: BT): BT = t match {
case Nil => Tree(Nil,x,Nil)
case Tree(left,value,right) if (x == value) => t
case Tree(left,value,right) if (x < value) =>
Tree(insertBST(x,left),value,right)
case Tree(left,value,right) if (x > value) =>
Tree(left,value,insertBST(x,right))
}
def toString(t: BT): String = t match {
case Nil => "nil"
case Tree(left,value,right) =>
"tree(" ++ toString(left) ++ "," ++
value.toString ++ "," ++ toString(right) ++ ")"
}
def printBST(s: BT): Unit = {
println(toString(s))
}
val nums = List(47,34,97,88,41,20,16,105,100,83,99,97)
val t3 = (nums foldLeft (Nil:BT))((t:BT,x:Int) => insertBST(x,t))
//println(t3)
println(memberBST(97,t3))
println(memberBST(96,t3))
Other Collections Objects¶
Class Hierarchy:
- Iterable
- Seq
- List, String, Array, Vector, Range
- Set
- Map
- Seq
Vector¶
A more balanced sequence; Faster random access to elements.
Very similar to lists otherwise.
val nums = Vector(1,2,3,4)
val people = Vector("Bob","James","Peter")
Vectors support same operations as lists except for ::
Instead of x :: xs, there is
x +: xs
which creates a new vector with lead element x followed by all elements of xs
xs :+ x
creates a new vector with trailing element x preceded by all elements of xs
Arrays, Strings, Ranges¶
Arrays and Strings support same operations as Seq and can be implicitly converted into Sequences whenever needed.
val xs : Array[Int] = Array(1,2,3)
xs map (x => 2 * x)
val ys: String = "Hello World"
// ys filter (x => x.isUpper)
ys filter (_.isUpper)
Ranges are sequences of evenly spaced integers (to, until, by keywords)
val r: Range = 1 until 5
val s: Range = 1 to 10
1 to 10 by 3
6 to 1 by -2
Some more Seq Operations¶
xs exists p
true if there is an element x in xs such that
p(x) is true, false otherwise
xs forall p
true if p(x) is true for all x in xs, false otherwise
xs zip ys
A sequence of pairs drawn from corresponding elements of
xs and ys
xs.unzip
reverse of zip
xs.flatMap f ( (xs map f).flatten )
Applies a collection generating function, f, to each
element of xs and returns a flat list by concatenating
the results
xs.sum
sum of all elements of xs
xs.product
product of all elements of xs
xs.max
max element of xs
xs.min
min element of xs
Examples¶
(1 to 3) map (x => (1 to 3) map (y => (x,y)))
(1 to 3) flatMap (x => (1 to 3) map (y => (x,y)))
def scalarProduct(xs: Vector[Double], ys: Vector[Double]): Double =
(xs zip ys).map(pair => pair._1 * pair._2).sum
scalarProduct(Vector(1,2,3),Vector(4,5,6))
def isPrime(n: Int): Boolean =
(2 until n/2) forall (d => n%d!= 0)
isPrime(13)
isPrime(15)
Nested Sequence Example¶
Given a positive integer, n, find all pairs of positive integers i and j with 1 <= j < i < n such that i + j is prime.
For example, if n = 7, the sought pairs will be
(2,1), (3,2), (4,1), (4,3), (5,2), (6,1), (6,5)
- Generate all pairs such that 1 <= j < i < n
- Filter the pairs for which i + j is prime.
// Generate Pairs:
val n = 7
val p = ((1 until n) map (i => (1 until i) map (j => (i, j))))
val pairs = ((1 until n) map (i => (1 until i) map (j => (i, j)))).flatten
// Using the law: xs flatMap f = (xs map f).flatten
val n = 7
val pairs = (1 until n) flatMap (i => (1 until i) map (j => (i, j)))
// Filter:
pairs filter (pair => isPrime(pair._1 + pair._2))
def primePair(n: Int): Seq[(Int,Int)] = {
val pairs = (1 until n) flatMap (i => (1 until i) map (j => (i, j)))
pairs.filter(pair => isPrime(pair._1 + pair._2))
}
primePair(7)
For Comprehensions¶
Higher order functions such as map, flatMap, or filter provide powerful
constructs to manipulate lists.
But sometimes these expressions become hard to understand. For example, the previous problem.
Scala’s for-comprehensions come to the rescue!
// Example:
class Student(n: String, a: Int) {
var name: String = n;
var age: Int = a;
}
val s1 = new Student("Jones",25)
val s2 = new Student("Smith",35)
var students = List(s1,s2)
for (s <- students if s.age > 30) yield s.name
For Comprehension Syntax¶
for ( s ) yield e
where s is a sequence of generators and filters and e is an expression
whose value is returned as an iterable.
A generator is of the form p <- e, where p is a pattern and e an expression
whose value is a collection.
A filter is of the form if f, where f is a boolean expression
The sequence must start with a generator.
instead of (s), we may write {s} if writing the for in multiple lines.
// Given a positive integer, n, find all pairs of positive
// integers i and j with 1 <= j < i < n such that i + j is prime.
for {
i <- 1 until n
j <- 1 until i
if isPrime(i+j)
} yield (i,j)
// Scalar Product
def scalarProduct(xs: Vector[Int], ys: Vector[Int]): Int =
(for ((x,y) <- (xs zip ys)) yield x * y).sum
scalarProduct(Vector(1,2,3),Vector(4,5,6))
Sets¶
Sets are another basic abstraction in the Scala collection.
val fruit = Set("apple","banana","pear")
val s = (1 to 6).toSet
val t = (5 to 9)
Most operations on sequences are also available on sets.
val s = (1 to 6).toSet
val t = (5 to 9)
val fruit = Set("apple","banana","pear")
s.map(x => x + 2)
s.map(_ + 2)
fruit filter(_.startsWith("app"))
s.nonEmpty
Main differences between sets and sequences:
- Sets are unordered
- Sets do not have duplicate elements
- Fundamental operation on sets is “contains” e.g. (s contains 5)
Set specific operations¶
println(s)
println(t)
s contains 6
s contains 8
s ++ t
n Queens problem¶
Given a n x n chess board, place n queens so that none of them are attacked by any other queen.
- Recursively solve for (k-1) queens
- Place kth queen such that it is not attacked by any of the previous queens
type Queen = (Int,Int)
type Solutions = List[List[Queen]]
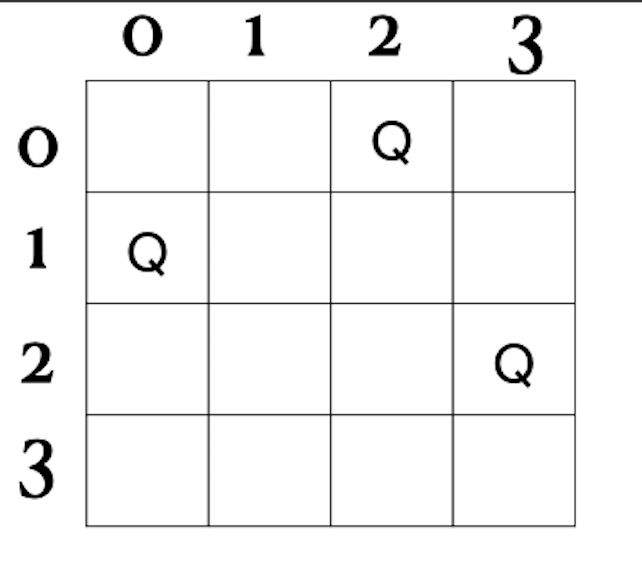
For example, if n=4, and let us say we have placed 3 queens already:
queens = List((0,2),(1,0),(2,3))
and we have to place the 4th queen. The choices will be
(3,0), (3,1), (3,2), (3,3)
For each, we have to verify it it is attacked by previous queens; and the correct choice will be
(3,1)
type Queen = (Int, Int)
type Solutions = List[List[Queen]]
def queens(n: Int) = {
def attacked(q1: Queen, q2: Queen) =
((q1._1 == q2._1) || (q1._2 == q2._2) ||
((q1._1-q2._1).abs == (q1._2-q2._2).abs))
def isSafe(queen: Queen, others: List[Queen]): Boolean =
others forall (x => !attacked(queen, x))
def placeQueens(k: Int): Solutions = {
if (k == 0) List[List[(Int,Int)]](List())
else
for {
queens <- placeQueens(k-1)
col <- 0 until n
if isSafe((k-1, col), queens)
} yield (k-1, col) :: queens
}
placeQueens(n)
}
queens(4)
Scala Maps (Dictionaries)¶
A Map consists of pairs of keys-values (also called mappings/associations)
key -> value
and
(key, value)
are treated the same.
val states1 = Map("AL" -> "Alabama", "AK" -> "Alaska")
creates an immutable Map
var states2 = scala.collection.mutable.Map("AL" -> "Alabama", "AK" -> "Alaska")
creates a mutable Map
To access a key/value pair:
states1("AL")
var states2 = scala.collection.mutable. Map("AL" -> "Alabama", "AK" -> "Alaska")
println(states2)
states2 += ("AZ" -> "Arizona", "CO" -> "Colorado")
println(states2)
states2 -= "AL"
println(states2)
states2 -= ("AZ","CO")
println(states2)
states2("AK") = "Alabama!"
println(states2)
Map methods¶
Lookups:
ms get k
The value associated with key k in map ms as an option, None if not found.
ms(k)
(or, written out, ms apply k) The value associated with key k in map ms, or exception if not found.
ms getOrElse (k, d)
The value associated with key k in map ms, or the default value d if not found.
ms contains k
Tests whether ms contains a mapping for key k.
ms isDefinedAt k
Same as contains.
Additions and Updates:
ms + (k -> v)
The map containing all mappings of ms as well as the mapping k -> v from key k to value v.
ms + (k -> v, l -> w)
The map containing all mappings of ms as well as the given key/value pairs.
ms ++ kvs
The map containing all mappings of ms as well as all key/value pairs of kvs.
ms updated (k, v)
Same as ms + (k -> v).
Removals:
ms - k
The map containing all mappings of ms except for any mapping of key k.
ms - (k, l, m)
The map containing all mappings of ms except for any mapping with the given keys.
ms -- ks
The map containing all mappings of ms except for any mapping with a key in ks.
Subcollections:
ms.keys
An iterable containing each key in ms.
ms.keySet
A set containing each key in ms.
ms.keysIterator
An iterator yielding each key in ms.
ms.values
An iterable containing each value associated with a key in ms.
ms.valuesIterator
An iterator yielding each value associated with a key in ms.
Transformation:
ms filterKeys p
A map view containing only those mappings in ms where the key satisfies predicate p.
ms mapValues f
A map view resulting from applying function f to each value associated with a key in ms.
Scala Maps and Frequency Counts¶
Given a text file, produce a frequency count of all characters in the file.
e.g. file a.txt contains
Upsets defined the NCAA tournament for most of the last two weeks, marking even more madness this March than usual. Sister Jean became the most famous nun in sports. A No. 16 seed (UMBC) topped a No. 1 seed (Virginia) for the first time in the men’s tournament. Buffalo busted brackets. So did Kansas State and Florida State and Syracuse.
import scala.io.Source
val s = Source.fromFile("a.txt").getLines.mkString.toUpperCase()
var fc = Map[Char,Int]() withDefaultValue 0
val freq = (s foldLeft fc)((m, c) => m updated (c, m(c)+1))
val ss = "abc"
ss.toUpperCase()