Lists

List is a fundamental data structure in functional programming.

List(x1,…,xn)

Examples:

val fruits = List("apple","banana","orange","mango")

val numbers = List(10,20,30)

val empty = List()

val nestedList = List(List(1,2,3),List(4,5),List(5,6,7))

Lists are immutable

Lists are recursive (i.e. nested)

LISP-like list structure: (Linked List with car-cdr)

Lists are homogenous. i.e. elements are of same type.

Type of a list of elements of type T is scala.List[T] or just List[T]

e.g.

val fruit: List[String] = List("apple","mango")

val nestedList: List[List[Int]] = 

    List(List(1,2,3),List(4,5))

val empty: List[Nothing] = List()

List Constructor

All lists are constructed from empty list Nil

construction operation :: (pronounced cons)

x :: xs gives a new list with first element x, followed by elements of list xs

e.g.

val fruit = "apple" :: ("orange" :: ("pear" :: Nil))

val nums = 1 :: (2 :: (3 :: (4 :: Nil)))

val empty = Nil

:: is right associative

A :: B :: C is interpreted as A :: (B :: C)

List Operations and Patterns

3 basic operations:

head - the first element of the list

tail - the list composed of all the elements except the first

isEmpty - true if list is empty, false otherwise

fruit.head == "apple"

fruit.tail.head == "orange"

empty.head == 
  throw new NoSuchElementException("head of empty list")

List Patterns

Nil

p :: ps

List(p1,…,pn)

1 :: 2 :: xs denotes a list whose first 2 elements are 1 and 2 and the rest of the list is xs

x :: Nil denotes a singleton list whose element is x

List(1 :: 2 :: xs) is a list of one element, which is the list 1,2,...

What can you say about the length of x :: y :: List(xs,ys) :: zs ?

Answer: >= 3

Sorting a list (insertion sort)

def isort(xs: List[Int]): List[Int] = xs match {
  case Nil => Nil
  case y :: ys => insert(y, isort(ys))
}

def insert(x: Int, xs: List[Int]): List[Int] = xs match {
  case Nil => x :: Nil
  case y :: ys => if (x <= y) x :: xs else y :: insert(x, ys)
}

// Time Complexity: O(n^2)

isort(List(10,9,8,12,5,9))

defined function isort
defined function insert
res0_2: List[Int] = List(5, 8, 9, 9, 10, 12)

Additional List Methods

Method	Meaning
xs.length	size of xs
xs.last	last element of xs, exception if xs is empty
xs.init	A list of all but the last element, exception if xs is empty
xs take n	List of first n elements, or xs if list is shorter than n
xs drop n	List of last n elements, or xs if list is shorter than n
xs(n)	or written xs apply n, element at index n

Creating new lists

Method	Meaning
xs ++ ys	concatenation
xs.reverse	reverse
xs updated (n,x)	update index n with x

Finding elements

Method	Meaning
xs indexOf x	index of x, -1 if not found
xs contains x	same as (xs indexOf x) >= 0)

val xs = List(1,2,3,4,5)
val ys = List(10,20,30)
xs.length
xs.last
xs.init
xs take 3
xs drop 2
xs(3)
xs apply 3

xs: List[Int] = List(1, 2, 3, 4, 5)
ys: List[Int] = List(10, 20, 30)
res1_2: Int = 5
res1_3: Int = 5
res1_4: List[Int] = List(1, 2, 3, 4)
res1_5: List[Int] = List(1, 2, 3)
res1_6: List[Int] = List(3, 4, 5)
res1_7: Int = 4
res1_8: Int = 4

xs ++ ys
xs.reverse
xs updated (3,99)
xs indexOf 4
xs contains 4
xs contains 98

res2_0: List[Int] = List(1, 2, 3, 4, 5, 10, 20, 30)
res2_1: List[Int] = List(5, 4, 3, 2, 1)
res2_2: List[Int] = List(1, 2, 3, 99, 5)
res2_3: Int = 3
res2_4: Boolean = true
res2_5: Boolean = false

Implementation of first, last, init

// Note use of templated functions! parameter T
def first[T](xs: List[T]): T = xs match {
    case Nil => throw new Exception("first of empty list")
    case y :: ys => y
}
// Time complexity: O(1)

def last[T](xs: List[T]): T = xs match {
    case Nil => throw new Exception("last of empty list")
    case x :: Nil => x
    case y :: z :: ys  => last(z :: ys)
}
// Time complexity of last: O(n)

def init[T](xs: List[T]): List[T] = xs match {
    case Nil => throw new Exception("init of empty list")
    case x :: Nil => Nil
    case y :: z :: ys  => y :: init(z :: ys)
} 
// Time complexity of last: O(n)

val xs = List(1,2,3,4,5)
first(xs)
last(xs)
init(xs)

defined function first
defined function last
defined function init
xs: List[Int] = List(1, 2, 3, 4, 5)
res3_4: Int = 1
res3_5: Int = 5
res3_6: List[Int] = List(1, 2, 3, 4)

Implementation of concat, reverse

def concat[T](xs: List[T], ys: List[T]): List[T] = xs match {
    case Nil     => ys
    case z :: zs => z :: concat(zs,ys)
} 
// Time complexity of last: O(|xs|)

def reverse[T](xs: List[T]): List[T] = xs match {
    case Nil     => Nil
    case y :: ys => reverse(ys) ++ List(y)
}
// Time complexity of last: O(n^2)
// Can be improved to O(n)!

concat(xs,ys)
reverse(xs)

defined function concat
defined function reverse
res4_2: List[Int] = List(1, 2, 3, 4, 5, 10, 20, 30)
res4_3: List[Int] = List(5, 4, 3, 2, 1)

Exercises:

Remove the nth element in a list (if no nth element, return original list)

def removeAt[T](xs: List[T], n: Int): List[T] = ???

removeAt(List(1,2,3,4),2)
res3: List[Int] = List(1, 3, 4)

Flatten a list structure

def flatten(xs: List[Any]): List[Any] = ???

flatten(List(List(1,2),3,List(4,5)))
res4: List[Any] = List(1, 2, 3, 4, 5)

Mergesort

def merge(xs: List[Int], ys: List[Int]): List[Int] = xs match {
  case Nil     => ys
  case x :: xt => ys match {
                    case Nil     => xs
                    case y :: yt => if (x < y) x :: merge(xt,ys) 
                                    else y :: merge(xs,yt)
                  }
}

def mergesort(xs: List[Int]): List[Int] = {
    val n = xs.length/2
    if (n == 0) xs
    else {
      val (first,second) = xs splitAt n // Tuple Data Structure     
      merge2(mergesort(first), mergesort(second))
    }
}

def merge2(xs: List[Int], ys: List[Int]): List[Int] = (xs,ys) match {
    case (Nil,Nil)     => Nil
    case (Nil,y::yt)   => ys
    case (x::xt,Nil)   => xs
    case (x::xt,y::yt) => if (x < y) x::merge(xt,ys) else y::merge(xs,yt)
}

val ts = List(3,1,9,12,4)
mergesort(ts)
// Can also access tuple elements as t._1, t._2, etc.

defined function merge
defined function mergesort
defined function merge2
ts: List[Int] = List(3, 1, 9, 12, 4)
res5_4: List[Int] = List(1, 3, 4, 9, 12)

Mergesort for lists of any type, List[T]

How to make mergesort more general?

def mergesort[T](xs: List[T]): List[T] = ???

The previous version will not work because of the < comparison in merge.

Lets send comparison as a parameter into mergesort/merge.

def mergesort[T](xs: List[T])(lt: (T,T) => Boolean): List[T] = {
    val n = xs.length/2
    if (n == 0) xs
    else {
        def merge(xs: List[T], ys: List[T]): List[T] = (xs,ys) match {
            case (Nil,Nil)     => Nil
            case (Nil,y::yt)   => ys
            case (x::xt,Nil)   => xs
            case (x::xt,y::yt) => if (lt(x,y)) x::merge(xt,ys) else y::merge(xs,yt)
        }
        val (first,second) = xs splitAt n
        merge(mergesort(first)(lt), mergesort(second)(lt))
    }
}

val xs = List(5,4,3,2)
val fruit = List("oranges","apples","bananas")
mergesort(xs)((x,y) => x < y)
mergesort(fruit)((x,y) => x.compareTo(y) < 0)

defined function mergesort
xs: List[Int] = List(5, 4, 3, 2)
fruit: List[String] = List("oranges", "apples", "bananas")
res6_3: List[Int] = List(2, 3, 4, 5)
res6_4: List[String] = List("apples", "bananas", "oranges")

Higher Order Functions for Lists

Some patterns in list processing:

• transform each element in a list in a particular way (map)

• retrieve subset of elements from a list (filter)

• combining elements of a list using an operator (reduce/fold)

Functional languages provide us higher-order functions to achieve these patterns

Map

// Consider the following function
def scaleList(xs: List[Double], factor: Double): List[Double] = xs match {
    case Nil     => Nil
    case y :: ys => y*factor :: scaleList(ys,factor)
}

scaleList(List(2.3, 4.5, 6.0), 2)

defined function scaleList
res7_1: List[Double] = List(4.6, 9.0, 12.0)

Actually, Scala Lists have a predefined operator, map, that can do this:

List(2.3, 4.5, 6.0).map(x => 3*x)

res8: List[Double] = List(6.8999999999999995, 13.5, 18.0)

The map function may be defined as follows: (SKIP!!)

abstract class List[T] {
  …
  def map[U](f: T=>U): List[U] = this match {
    case Nil => this
    case x :: xs => f(x) :: xs.map(f)
  }
  …
}

def squareList(xs: List[Int]): List[Int] = xs match {
    case Nil     => Nil
    case y :: ys => y*y :: squareList(ys)
}

def squareList2(xs: List[Int]): List[Int] = 
    xs.map(x=>x*x)
                                                 
squareList(List(1,3,6)) 
                       
squareList2(List(1,3,6))

defined function squareList
defined function squareList2
res9_2: List[Int] = List(1, 9, 36)
res9_3: List[Int] = List(1, 9, 36)

Filter

def posElements(xs: List[Int]): List[Int] = xs match {
    case Nil => Nil
    case y :: ys => if (y > 0) y :: posElements(ys) else posElements(ys)
}

posElements(List(-1,1,2,-3,5))

defined function posElements
res10_1: List[Int] = List(1, 2, 5)

Actually, Scala Lists have a predefined operator, called filter:

List(-1,1,2,-3,5) filter (x => x > 0)

res11: List[Int] = List(1, 2, 5)

List(-1,1,2,-3,5) map (x => x > 0)

res12: List[Boolean] = List(false, true, true, false, true)

The filter function may be defined as follows: (SKIP!!)

abstract class List[T] {
…
  def filter(p: T=>Boolean): List[T] = this match {
    case Nil => this
    case x :: xs => if (p(x)) x:: xs.filter(p) 
                    else filter(p)
  }
…
}

Variations of the filter operator

xs filterNot p same as xs filter (x => !p(x))

xs partition p same as

(xs filter (x => p(x)), xs filterNot (x => p(x))

xs takeWhile p longest prefix of xs such that the elements satisfy p

xs dropWhile p remaining list after all leading elements satisfying p are dropped

xs span p same as

(xs takenWhile (x => p(x)), xs dropWhile (x => p(x))

Using map to pack/encode

def pack[T](xs: List[T]): List[List[T]] = xs match {
    case Nil     => Nil
    case y :: ys => pack(ys) match {
                      case Nil     => List(List(y))
                      case z :: zs => 
                         if (z contains y) (y :: z) :: zs 
                         else List(y) :: z :: zs
                    }
}                                              

val xs = List("a","a","a","b","c","c","a")
// y = "a"
// ys = List("a","a","b","c","c","a")
// pack(ys) = List(List("a","a"),List("b"),List("c","c"),List("a"))
// z = List("a","a")
// zs = List(List("b"),List("c","c"),List("a")) 
pack(xs)

defined function pack
xs: List[String] = List("a", "a", "a", "b", "c", "c", "a")
res13_2: List[List[String]] = List(
  List("a", "a", "a"),
  List("b"),
  List("c", "c"),
  List("a")
)

def encode[T](xs: List[T]): List[(T,Int)] =
  pack(xs).map(x => x match {case a::as => (a,(a::as).length)})
                                                     
encode(List("a","a","a","b","c","c","a"))       

encode(List())

defined function encode
res14_1: List[(String, Int)] = List(("a", 3), ("b", 1), ("c", 2), ("a", 1))
res14_2: List[Tuple2[Nothing, Int]] = List()

Reduce

Combine elements in a list using a given operator.

sum(List(x1,…,xn)) = 0 + x1 + … + xn

product(List(x1,…,xn)) = 1 * x1 * …* xn

We could implement this using recursion as follows:

def sum(xs: List[Int]): Int = xs match {
  case Nil => 0
  case y :: ys => y + sum(ys)
}

sum(List(2,4,6,8))

defined function sum
res15_1: Int = 20

But, Scala provides an operator, reduceLeft, to do this:

def sum(xs: List[Int]): Int = 
    (0 :: xs) reduceLeft ((x,y) => x + y)

def product(xs: List[Int]): Int = 
    (1 :: xs) reduceLeft ((x,y) => x * y)

sum(List(3,10,2,5))
product(List(3,10,2,5))

defined function sum
defined function product
res16_2: Int = 20
res16_3: Int = 300

Shorter way to write anonymous functions:

(_*_) is the same as ((x,y) => (x * y))

Every _ represents a new parameter, going from left to right.

def sum(xs: List[Int]): Int = 
    (0 :: xs) reduceLeft (_+_)

def product(xs: List[Int]): Int = 
    (1 :: xs) reduceLeft (_*_)

sum(List(2,4,6,8))
product(List(2,4,6,8))

defined function sum
defined function product
res17_2: Int = 20
res17_3: Int = 384

Fold

fold is similar to reduce, but takes an accumulator, x, as an additional parameter; the accumulator is returned when called with an empty list.

(List(x1,…,xn) foldLeft acc)(op) = (…(acc op x1) op … ) op xn

So, sum and product can be written as:

def sum(xs: List[Int]): Int = 
    (xs foldLeft 0)(_+_)

def product(xs: List[Int]): Int = 
    (xs foldLeft 1)(_*_)

reduceLeft and foldLeft may be implemented within List class as follows: SKIP!!

abstract class List[T] {…
  def reduceLeft(op: (T,T)=>T): T = this match {
    case Nil => throw new Error("Nil reduceLeft")
    case x :: xs => (xs foldLeft x)(op)
  }
  def foldLeft[U](acc: U)(op: (U,T) => U): U = this match {
    case Nil => acc
    case x :: xs => (xs foldLeft op(acc,x))(op)
  }
}

(5::Nil reduceLeft (_+_))
(5::Nil foldLeft 0) (_+_)

res18_0: Int = 5
res18_1: Int = 5

reduceRight and foldRight

List(x1,…,xn-1,xn) reduceRight op = 
    x1 op (x2 op (…(xn-1 op xn)…)

(List(x1,…,xn) foldRight acc)(op) = 
    x1 op (…(xn op acc)…)

reduceRight and foldRight may be implemented within List class as follows: SKIP!!

abstract class List[T] {…
  def reduceLeft(op: (T,T)=>T): T = this match {
    case Nil      => throw new Error("Nil reduceRight")
    case x :: Nil => x
    case x :: xs  => op(x, xs reduceRight(op))
  }
  def foldRight[U](z: U)(op: (U,T) => U): U = this match {
    case Nil     => z
    case x :: xs => op(x, (xs foldRight z)(op))
  }
}

For operators that are associative and commutative, foldLeft and foldRight are equivalent. But is some cases one is more appropriate than the other.

e.g.

def concat[T](xs: List[T], ys: List[T]): List[T] = 
    (xs foldRight ys)(_ :: _)

reverse, mapFun, lengthFun

def reverse[T](xs: List[T]): List[T] =  
    (xs foldLeft List[T]())((ys, y) => y :: ys )

// Time Complexity O(n)

reverse(List(1,2,3,4,5))

defined function reverse
res19_1: List[Int] = List(5, 4, 3, 2, 1)

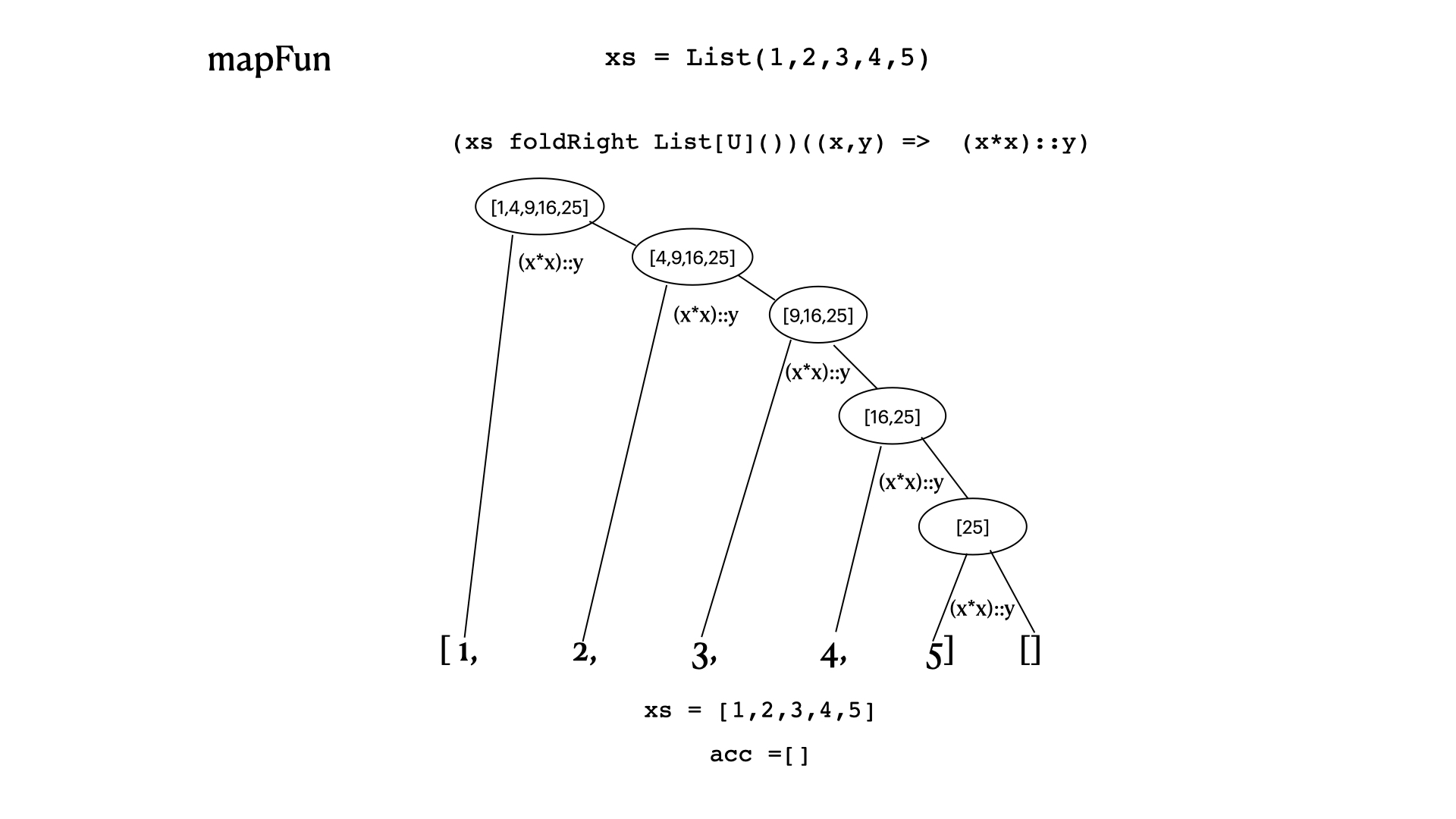
def mapFun[T,U](xs: List[T], f: T => U): List[U] =
  (xs foldRight List[U]())((x, y) => f(x)::y)   
    
mapFun(List(1,2,3,4,5), (x => x * x): Int =>Int )

defined function mapFun
res20_1: List[Int] = List(1, 4, 9, 16, 25)

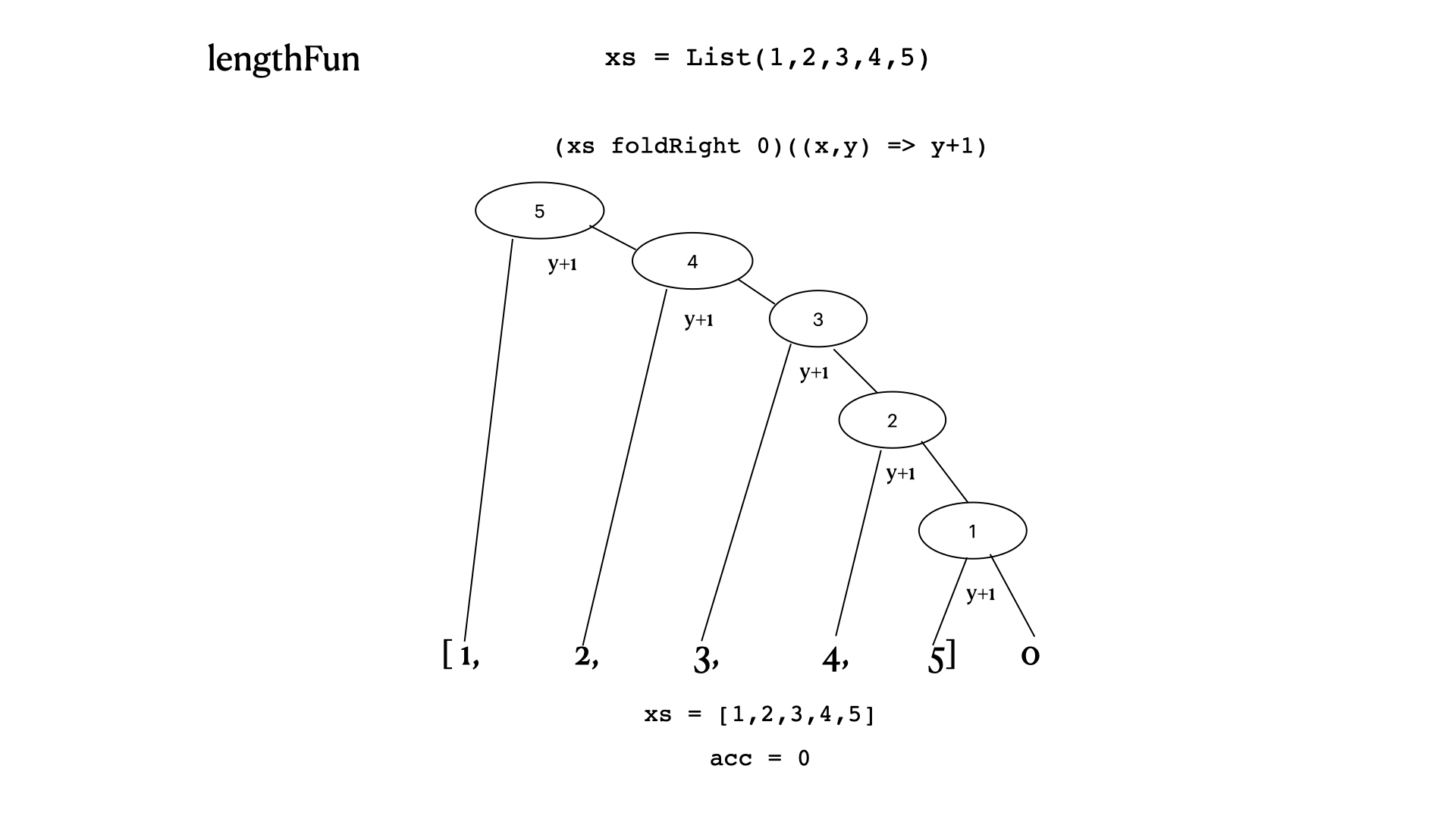
def lengthFun[T](xs: List[T]): Int =
  (xs foldRight 0)((x, y) => y+1)                 

lengthFun(List(1,2,3,4,5))

defined function lengthFun
res21_1: Int = 5